ESTADISTICAS PARA DESARROLLAR EL MODELO
Este trabajo fue efectuado con la ayuda de un poderoso software de estadística STATGRAFIC, que junto con el software The Economist System nos ayudara en la contracción de un modelo para PIB con respecto al consumo de energía.
1.- A partir de la ecuación económica mundial
PIB = CONSUMO + INVERSION + GASTO PUBLICO + EXPORTACIOMES – IMPORTACIONES.
Determinamos la primera ecuación de nuestro modelo
2- Para determinar el Consumo, hacemos una regresión lineal entre los datos del consumo (variable dependiente) y el PIB (variable independiente) ya que sabemos que tienen una dependencia económica, los análisis estadísticos son los siguientes:
|
AÑO |
CONSUMO TOTAL |
PIB TOTAL
|
|
1990 |
12.040.489 |
25.715.700 |
|
1991 |
13.687.555 |
26.721.130 |
|
1992 |
15.324.088 |
27.726.560 |
|
1993 |
16.958.755 |
28.731.990 |
|
1994 |
18.607.754 |
29.737.420 |
|
1995 |
20.249.536 |
30.742.850 |
|
1996 |
21.329.192 |
31.237.289 |
|
1997 |
23.834.532 |
33.300.693 |
|
1998 |
25.802.168 |
34.376.598 |
|
1999 |
26.193.915 |
34.115.042 |
|
2000 |
28.519.087 |
35.646.492 |
|
2001 |
29.027.868 |
36.854.918 |
|
2002 |
30.332.248 |
37.670.155 |
|
|
|
|
|
|
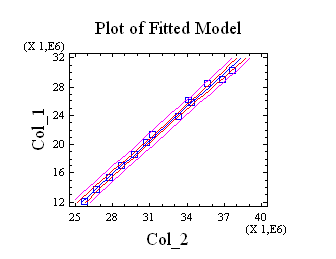
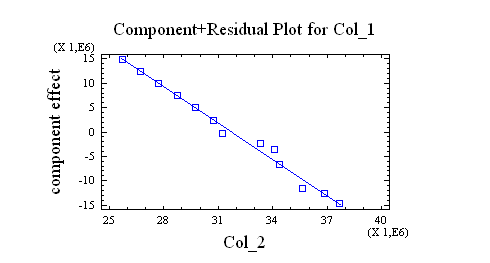
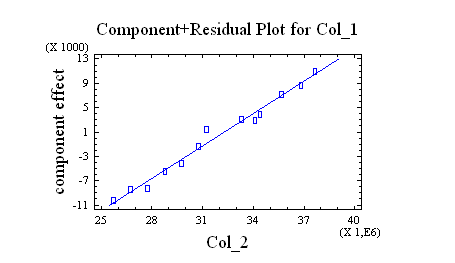
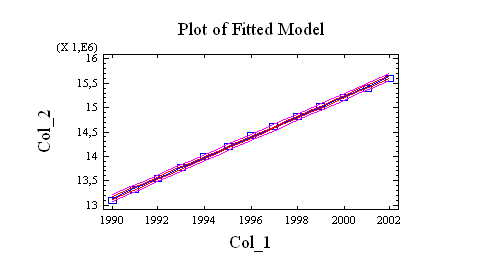
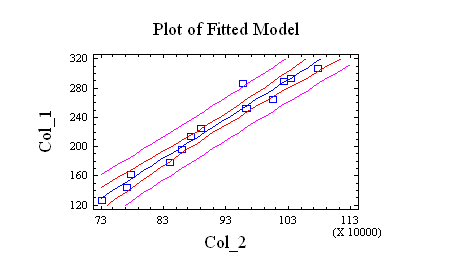
El
gráfico asociado a estos datos es:
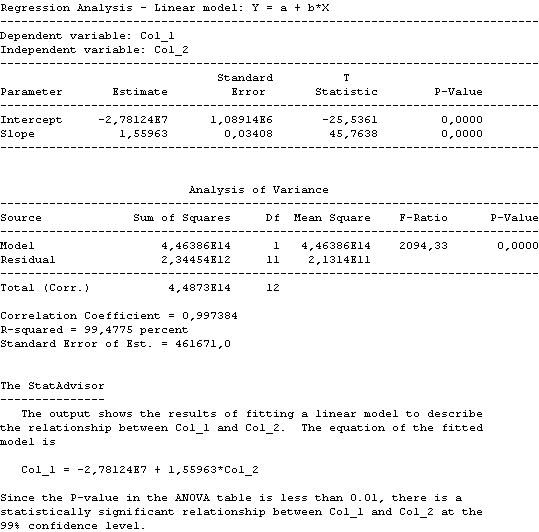
El modelo queda de la forma:
CONSUMO TOTAL = -2.78124E7 + 1.55963 * PIB TOTAL
Que posee un margen de error de P-value de un 0.01% y un nivel de confianza en el modelo de un 99% que es estadísticamente aceptable.
*****3.- Para determinar la Inversión Total, hacemos una regresión múltiple entre los datos de la Inversión Total (variable dependiente) y el PIB, la Tasa de Interés y Gasto Público (variables independientes) ya que sabemos que estas variables son económicamente dependientes, los análisis estadísticos son los siguientes :
|
AÑO |
INVERSION TOTAL |
PIB TOTAL |
TASA DE INTERES |
GASTO PUBLICO TOTAL |
|
1990 |
5,507,380 |
25,715,700 |
8.23 |
1,940,252 |
|
1991 |
5,369,841 |
26,721,130 |
8.05 |
2,616,501 |
|
1992 |
5,204,733 |
27,726,560 |
7.87 |
3,285,187 |
|
1993 |
5,076,432 |
28,731,990 |
7.71 |
3,960,585 |
|
1994 |
4,842,570 |
29,737,420 |
7.51 |
4,613,795 |
|
1995 |
4,614,800 |
30,742,850 |
7.33 |
5,265,291 |
|
1996 |
4,821,872 |
31,237,289 |
6.94 |
6,138,959 |
|
1997 |
5,229,822 |
33,300,693 |
6.45 |
6,910,806 |
|
1998 |
5,972,694 |
34,376,598 |
9.53 |
7,785,208 |
|
1999 |
9,085,647 |
34,115,042 |
5.87 |
8,425,975 |
|
2000 |
2,997,519 |
35,646,492 |
5.17 |
9,073,104 |
|
2001 |
7,197,338 |
36,854,918 |
8.59 |
9,915,574 |
|
2002 |
7,175,035 |
37,670,155 |
8.41 |
10,494,139 |
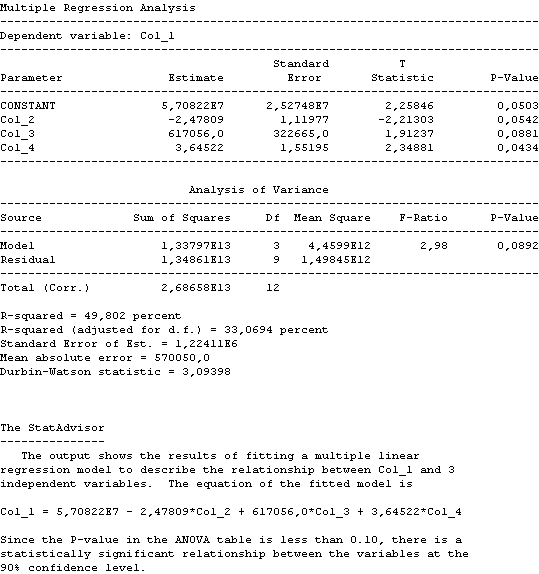
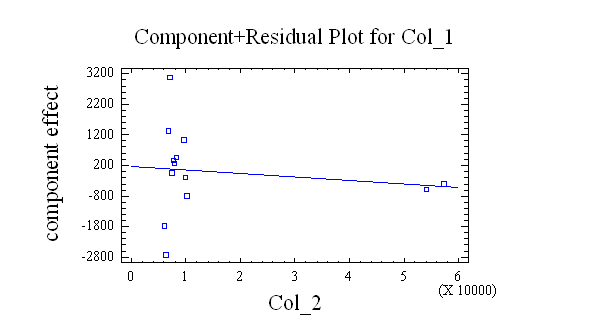
El gráfico asociado a estos datos es:
|
|
|
|
|
|
El modelo queda de la forma:
INVERSION TOTAL = 5.70822E7 – 2.4809*PIB TOTAL + 6.17056*TASA DE INTERES + 3.64 522 *GASTO PUBLICO TOTAL
Posee un margen de error de P-value de un 0.0892% y un nivel de confianza en el modelo de un 90% que es estadísticamente aceptable.
4.- El Gasto Público Total está dado por la variable exógena que entrará a nuestro modelo.
Gasto Publico = Gasto Publico
5.- Para determinar las Exportaciones Cupreras, hacemos una regresión múltiple entre los datos de las Exportaciones Cupreras (variable dependiente) y Miles de toneladas de Cobre Anual con el Precio Promedio de la Libra de Cobre (variables independientes) ya que sabemos que estas variables son económicamente dependiente lo que da como resultado:
|
AÑO |
EXPORTACIONES DE COBRE |
MILES DE TONELADAS EXPORTADAS |
PRECIO DE LA LIBRA DE COBRE |
|
1990 |
3.810,20 |
39.586 |
92,5 |
|
1991 |
3.617,30 |
39.895 |
93,8 |
|
1992 |
3.886,00 |
40.258 |
94,1 |
|
1993 |
3.247,80 |
41.118 |
95,3 |
|
1994 |
4.242,00 |
52.090 |
113,9 |
|
1995 |
6.487,10 |
54.668 |
139,6 |
|
1996 |
6.028,60 |
52.716 |
110,4 |
|
1997 |
6.840,80 |
48.804 |
109,7 |
|
1998 |
5.331,60 |
49.733 |
176,8 |
|
1999 |
5.888,50 |
55.221 |
171,9 |
|
2000 |
7.346,60 |
58.707 |
124,8 |
|
2001 |
7.554,20 |
69.122 |
69,9 |
|
2002 |
7.948,80 |
67.050 |
70,6 |

El gráfico asociado a estos datos es:
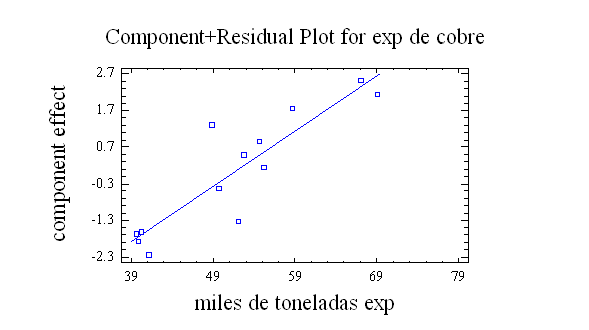
El modelo queda de la forma:
Exp. De Cobre = -2.54731 + 0.150426*miles de toneladas exp. +0.000322164*Precio libra de cobre
Posee un margen de error de P-value de un 0.0003% y un nivel de confianza en el modelo de un 97% que es estadísticamente aceptable.
6.-- Para determinar las Exportaciones Totales utilizamos la ecuación económica:
EXPORTACIONES TOTALES = EXPORTACIONES CUPRERAS + EXPORTACIONES NO CUPRERAS
7.- Para determinar las Exportaciones no Cupreras, hacemos una regresión múltiple entre los datos de las Exportaciones No Cupreras (variable dependiente) con el PIB USA y el Tipo de Cambio Real (variables independientes) ya que sabemos que estas variables son económicamente dependiente, el análisis estadístico es el siguiente:
|
|
Exp. No Cuprina |
PIB USA |
Tipo cambio |
|
AÑO |
mill US$ |
mill de US$ |
real |
|
|
|
|
|
|
1990 |
10,005.28 |
54162.1 |
368.98 |
|
1991 |
10,229.90 |
57345.6 |
399.45 |
|
1992 |
8,807.78 |
6058.05 |
362.58 |
|
1993 |
7,896.07 |
6387.69 |
404.17 |
|
1994 |
11,980.67 |
6737.37 |
420.18 |
|
1995 |
13,702.84 |
7100.01 |
396.77 |
|
1996 |
10,598.20 |
7433.52 |
412.27 |
|
1997 |
11,029.40 |
7783.1 |
419.31 |
|
1998 |
10,991.20 |
7903 |
460.29 |
|
1999 |
11,273.70 |
8351 |
508.78 |
|
2000 |
11,863.70 |
9646 |
539.49 |
|
2001 |
10,717.60 |
9900 |
590.58 |
|
2002 |
10,228.50 |
10200 |
658.96 |

El gráfico asociado a estos datos es:
El modelo queda de la forma:
Exp. No Cuprinas = 10198.7 – 0.0111597*PIB de USA + 1.50849*Tipo de Cambio Real
8.- Para determinar las Importaciones Totales, hacemos una regresión múltiple entre los datos de las Importaciones Totales (variable dependiente) y el PIB total con el Tipo de Cambio Real (variables independientes) ya que sabemos que estas variables son económicamente dependiente, el análisis estadístico es el siguiente :
|
AÑO |
IMPORTACIONES TOTALES |
PIB TOTAL |
TIPO CAMBIO REAL |
|
1990 |
7.089,20 |
25.715.700 |
368,98 |
|
1991 |
7.456,40 |
26.721.130 |
399,45 |
|
1992 |
9.285,40 |
27.726.560 |
362,58 |
|
1993 |
10.188,50 |
28.731.990 |
404,17 |
|
1994 |
10.872,10 |
29.737.420 |
420,18 |
|
1995 |
14.642,50 |
30.742.850 |
396,77 |
|
1996 |
16.810,00 |
31.237.289 |
412,27 |
|
1997 |
18.112,00 |
33.300.693 |
419,31 |
|
1998 |
17.087,00 |
34.376.598 |
460,29 |
|
1999 |
14.022,00 |
34.115.042 |
508,78 |
|
2000 |
16.832,00 |
35.646.492 |
539,49 |
|
2001 |
16.160,00 |
36.854.918 |
590,58 |
|
2002 |
15.445,00 |
37.670.155 |
658,96 |

El gráfico asociado a estos datos es:
|
|
|
|
|
|
El modelo queda de la forma:
IMPORTACIONES TOTALES = -22097.2 + 0.00175666*PIB TOTAL –44.3455*TIPO CAMBIO REAL
Y posee un margen de error de P-value de un 0.01% y un nivel de confianza en el modelo de un 99% que es estadísticamente aceptable.
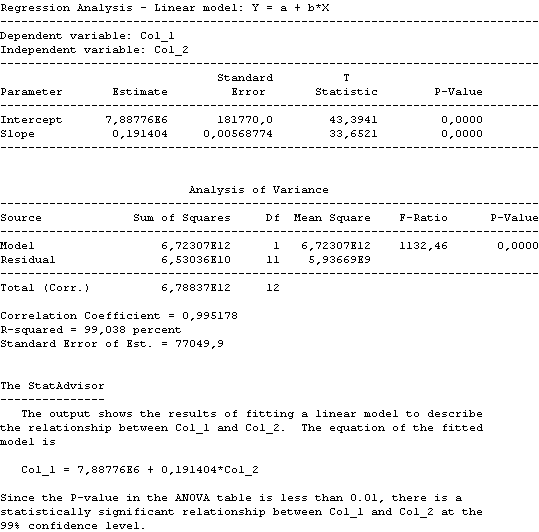
9.- Para determinar el Empleo Total, hacemos una regresión lineal entre los datos de Empleo Total (variable dependiente) y el PIB total (variable independiente) ya que sabemos que estas variables son económicamente dependiente, el análisis estadístico es el siguiente:
|
AÑO |
EMPLEO TOTAL |
PIB TOTAL |
|
1990 |
12.726.063 |
25.715.700 |
|
1991 |
12.916.926 |
26.721.130 |
|
1992 |
13.208.054 |
27.726.560 |
|
1993 |
13.425.355 |
28.731.990 |
|
1994 |
13.569.248 |
29.737.420 |
|
1995 |
13.805.271 |
30.742.850 |
|
1996 |
14.060.993 |
31.237.289 |
|
1997 |
14.278.550 |
33.300.693 |
|
1998 |
14.469.167 |
34.376.598 |
|
1999 |
14.453.191 |
34.115.042 |
|
2000 |
14.671.917 |
35.646.492 |
|
2001 |
14.865.251 |
36.854.918 |
|
2002 |
15.059.759 |
37.670.155 |
El gráfico asociado a estos datos es :
|
|
|
|
|
|
El modelo queda de la forma:
EMPLEO TOTAL = 7.88776E6 + 0.191404*PIB TOTAL
Y posee un margen de error de P-value de un 0.01% y un nivel de confianza en el modelo de un 99% que es estadísticamente aceptable.
10.- Para determinar la Población Total, hacemos una regresión lineal entre los años (variable independiente) y la Población Total (variable dependiente) ya que sabemos que estas variables son dependiente, el análisis estadístico es el siguiente :
|
AÑO |
POBLACION TOTAL |
|
1990 |
13.099.513 |
|
1991 |
13.319.726 |
|
1992 |
13.544.964 |
|
1993 |
13.771.187 |
|
1994 |
13.994.355 |
|
1995 |
14.210.429 |
|
1996 |
14.418.864 |
|
1997 |
14.622.354 |
|
1998 |
14.821.714 |
|
1999 |
15.017.760 |
|
2000 |
15.211.308 |
|
2001 |
15.401.952 |
|
2002 |
15.589.147 |
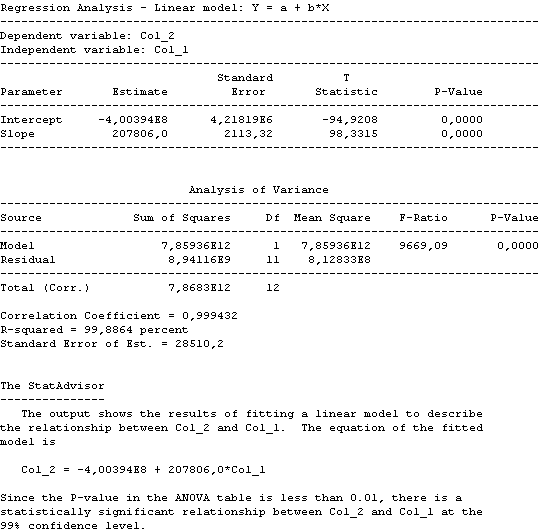
El gráfico asociado a estos datos es:
|
|
|
|
|
|
El modelo queda de la forma:
POBLACION TOTAL = -4.00394E8 + 207806.0*AÑO
Y posee un margen de error de P-value de un 0.01% y un nivel de confianza en el modelo de un 99% que es estadísticamente aceptable.
Pero por otro lado no tenemos dentro de nuestras variables los años asi que el programa no reconoce esta ecuación (se intento) así que usamos la ecuación:
Población Total = Población total
Donde la primera sale de las variables endógenas y la segunda de las variables exógenos.
11.- Para determinar el PIB en energía, para ello adaptamos la ecuación económica mundial del PIB, pero ahora hacia la energía:
PIB Energía = Consumo de Energía + Inversión en Energía + Gasto Publico en energía + Exp. Totales de energía – Importaciones Totales de energía
No hay que olvidar que Chile no exporta energía, así que la ecuación nos queda de la siguiente manera:
PIB Energía = Consumo de Energía + Inversión en Energía + Gasto Publico en Energía – Importaciones de Energía
12.- Para determinar el Consumo de Energía, hacemos una regresión lineal entre los datos del Consumo de Energía (variable dependiente) y el PIB de Energía (variable independiente), el análisis estadístico es el siguiente :
|
AÑO |
CONSUMO DE ENERGIA |
PIB ENERGIA |
|
1990 |
126,838 |
732.167 |
|
1991 |
144,188 |
772.726 |
|
1992 |
161,438 |
778.384 |
|
1993 |
178,617 |
840.382 |
|
1994 |
196,019 |
859.951 |
|
1995 |
213,487 |
875.298 |
|
1996 |
224,688 |
889.376 |
|
1997 |
252,168 |
962.995 |
|
1998 |
264,754 |
1.005.482 |
|
1999 |
286,266 |
957.735 |
|
2000 |
288,481 |
1.023.089 |
|
2001 |
293,627 |
1.033.226 |
|
2002 |
306,821 |
1.077.121 |
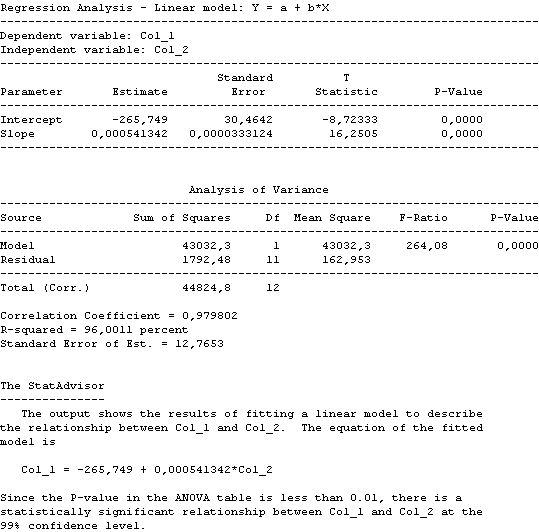
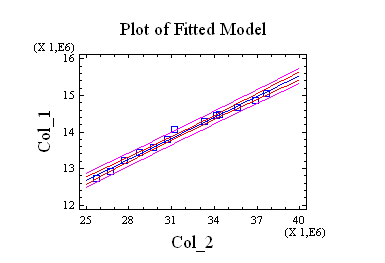
El gráfico asociado a estos datos es:
|
|
|
|
|
|
El modelo queda de la forma:
CONSUMO DE ENERGIA = -2.78124E7 + 1.55963 * PIB ENERGIA
Que posee un margen de error de P-value de un 0.01% y un nivel de confianza en el modelo de un 99% que es estadísticamente aceptable.
******************13.- Para determinar la Inversión en Energía, hacemos una regresión múltiple entre los datos de la Inversión en Energía (variable dependiente) y el PIB de Energía , la Tasa de Interés y Gasto Público en Energía (variables independientes) ya que sabemos que estas variables son económicamente, los análisis estadístico es el siguiente :
|
AÑO |
INVERSION EN ENERGIA |
PIB ENERGIA |
TASA DE INTERES |
GASTO PUBLICO EN ENERGIA |
|
1990 |
1.103.358 |
732.167 |
8,23 |
50.194 |
|
1991 |
997.457 |
772.726 |
8,05 |
67.688 |
|
1992 |
870.398 |
778.384 |
7,87 |
84.987 |
|
1993 |
771.540 |
840.382 |
7,71 |
102.460 |
|
1994 |
594.476 |
859.951 |
7,51 |
119.358 |
|
1995 |
416.096 |
875.298 |
7,33 |
136.218 |
|
1996 |
406.047 |
889.376 |
6,94 |
158.784 |
|
1997 |
1.394.712 |
962.995 |
6,45 |
178.247 |
|
1998 |
495.016 |
1.005.482 |
9,53 |
201.785 |
|
1999 |
4.559.719 |
957.735 |
5,87 |
217.951 |
|
2000 |
859.772 |
1.023.089 |
5,17 |
234.784 |
|
2001 |
2.404.578 |
1.033.226 |
8,59 |
256.547 |
|
2002 |
2.387.406 |
1.077.121 |
8,41 |
274.158 |

El gráfico asociado a estos datos es:
|
|
|
|
|
|
El modelo queda de la forma:
INVERSION EN ENERGIA = 2.1398E7 – 315367*PIB ENERGIA - 20130*TASA DE INTERES + 54.4531*GASTO PUBLICO EN ENERGIA
Posee un margen de error de P-value de un 0.0553% y un nivel de confianza en el modelo de un 90% que es estadísticamente aceptable.
14.- El Gasto Público En Energía está dado por la variable exógena que entrará a nuestro modelo.
Gasto Publico en Energía = Gasto Publico en Energía
15.- Para determinar las Importaciones de Energía, hacemos una regresión múltiple entre los datos de las Importaciones de Energía (variable dependiente) y el PIB Energía con el Tipo de Cambio Real (variables independientes) ya que sabemos que estas variables son económicamente dependiente, el análisis estadístico es el siguiente :
|
AÑO |
IMP ENERGIA |
PIB ENERGIA |
TIPO CAMBIO REAL |
|
1990 |
1,514 |
732,167 |
368.98 |
|
1991 |
1,553 |
772,726 |
399.45 |
|
1992 |
1,746 |
778,384 |
362.58 |
|
1993 |
1,841 |
840,382 |
404.17 |
|
1994 |
1,912 |
859,951 |
420.18 |
|
1995 |
2,091 |
875,298 |
396.77 |
|
1996 |
2,538 |
889,376 |
412,27 |
|
1997 |
2,675 |
962,995 |
419,31 |
|
1998 |
2,567 |
1,005,482 |
460,29 |
|
1999 |
2,243 |
957,735 |
508,78 |
|
2000 |
2,540 |
1,023,089 |
539,49 |
|
2001 |
2,469 |
1,033,226 |
590.58 |
|
2002 |
2,394 |
1,077,121 |
658.96 |
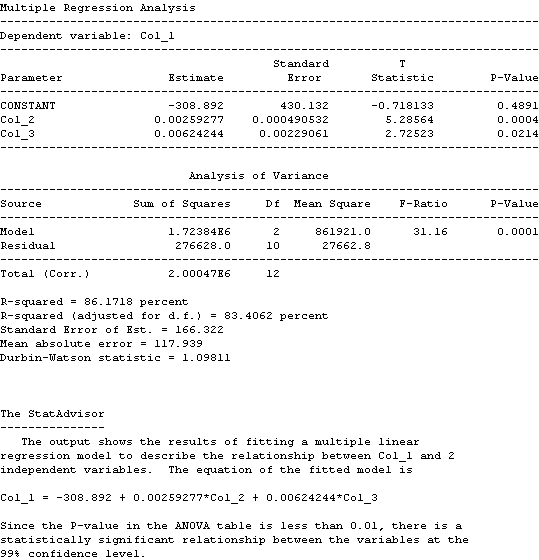
El gráfico asociado a estos datos es:

El modelo queda de la forma:
IMPORTACIONES DE ENERGIA= -308.892 + 0.00259277*PIB ENERGIA + 0.00624244*TIPO CAMBIO REAL
Y posee un margen de error de P-value de un 0.01% y un nivel de confianza en el modelo de un 99% que es estadísticamente aceptable.